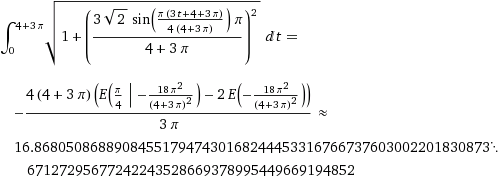Mathematics notes

Sikloid merupakan salah satu jenis kurva yang sangat terkenal (lihat saja ia mempunyai nama khusus), selain itu yang membuat kurva ini meraih popularitas adalah beberapa nama matematikawan besar dunia telah berkerja dalam pencarian solusi berkenaan dengan permasalahan yang berhubungan dengan sikloid. Sikloid bisa dipahami secara fisik sebagai kurva jejak dari sebuah titik pada tepian roda, ketika roda tersebut menggelinding (melakukan gerak translasi dan rotasi dalam waktu yang bersamaan) pada suatu lintasan lurus.

Cukup sulit dibayangkan, ilustrasi ini akan sangat membantu.

Dalam kuliah kalkulkus telah kita ketahui bahwa kurva sikloid yang dibangun oleh lingkaran berjari-jari r, memiliki persamaan parametrik sebagai berikut:

$x = r(t - \sin t)\,$

$y = r(1 - \cos t)\,$

dengan t merupakan parameter real.

Kebanyakan para matematikawan dulu bersusah payah mencari luas daerah dibawah kurva ini dengan berbagai pendekatan sebut saja Galileo (1564-1642), Roberval (1602-1675), Cavalieri (1598-1647), Fermat (1601-1665) dan Descartes (1596-1650). Hingga akhirnya Blaise Pascal (1623-1662) menutup masalah pencarian luas ini dalam sebuah paper berjudul "L'Histoire de la Roulette". Masih banyak pertanyaan seputar kurva ini yang bisa dimunculkan, salah satunya adalah panjang kurva itu sendiri. Perhitungan panjang dari jejak roda (sikloid) ini mungkin dilakukan dengan memanfaatkan rumus integral untuk panjang kurva yaitu,

$L=\int_{a}^{b}\sqrt{\left ( \frac{dx}{dt} \right )^{2}+\left ( \frac{dy}{dt} \right)^2}dt$

Perhitungan panjang kurva ini banyak dijumpai dalam buku teks kalkulus, sehingga saya tidak akan menulis ulang di blog ini. Namun, saya akan membahas tentang suatu masalah yang tidak terpecahkan dalam suatu sesi kuliah yang saya ikuti beberapa minggu lalu, yaitu bagaimana jika sebuah batang yang lebih panjang dari jari-jari roda, ditempatkan sebagai jari-jari roda, berapa panjang kurva yang terbentuk?

Batang 'biru' membuat jejak 'merah' yang membentuk sikloid ketika roda menggelinding

Untuk menjawab pertanyaan diatas, adalah perlu menentukan persamaan parametrik untuk kurva ini, agar kita dapat menerapkan rumus integral untuk panjang kurva (L).

Kondisi awal

Disini batang dan jari-jari memiliki panjang yang fix, masing-masing r dan m, sedangkan sudut a merupakan variabel bergantung, begitu pula dengan r tan(a). Sebelum lebih jauh, kita akan menghitung laju perubahan elevasi sudut a (hanya pada separuh pergerakan roda), mengingat bentuk kurva yang simetris. Terlihat bahwa roda akan menempuh sudut sebesar $\inline \pi -a$ , sehingga proyeksi ujung batang pada sumbu x telah menempuh r tan(a) juga separuh dari perpindahan pusat roda $\inline r(\pi -a)$ . Akibatnya besar sudut yang telah ditempuh tiap unit pada sumbu x dapat dinyatakan sebagai,

$\kappa =\frac{\pi -a}{rtan(a)+r(\pi -a)}$

Sehingga interval dari parameter t yang dipilih adalah $\inline [0, rtan(a)+r(\pi -a)]$ .

Fungsi x(t) dan y(t) merupakan fungsi posisi

Mula-mula kita definisikan laju perubahan sudut a dalam fungsi t:

$a(t)=\kappa t+a$

$a(t)=(\frac{\pi -a}{rtan(a)+r(\pi -a)}) t+a$

sehingga,

$x(t)=t$

Untuk fungsi y(t) perhatikan sketsa berikut:

Posisi roda pada waktu tertentu

sehingga didapat fungsi y(t),

$y(t)=r+m sin(a(t)-\frac{\pi}{2} )$

karena r tan(a) bergantung pada m dan r, dengan memanfaatkan Phytagoras ianya dapat dinyatakan sebagai,

$rtan(a)=\sqrt{m^{2}-r^{2}}=n$

Sehingga semua kekacauan diatas dapat kita tata sebagai berikut:

$a(t)=(\frac{\pi -a}{n+r(\pi -a)}) t+a$

$x(t)=t$

$y(t)=r-mcos(a(t))=r-mcos((\frac{\pi -a}{n+r(\pi -a)}) t+a)$

$0\leq t\leq n+r(\pi -a)$

Namun untuk menentukan panjang kurva, kita memerlukan fungsi turunan dari fungsi parametrik ini, untuk fungsi x(t) sepertinya tidak ada masalah, namun untuk y(t) sepertinya kita perlu sedikit menerapkan aturan rantai untuk mendapatkan fungsi turunannya.

$\frac{\mathrm{d}x }{\mathrm{d} t}=1$

$\frac{\mathrm{d} y}{\mathrm{d} t}=\frac{msin(\frac{(\pi -a)t}{n+r(\pi -a)}+a)(\pi -a)}{n+r(\pi -a)}$

Perhitungan Panjang Kurva

$L=\int_{a}^{b}\sqrt{\left ( \frac{dx}{dt} \right )^{2}+\left ( \frac{dy}{dt} \right)^2}dt$

$L=\int_{0}^{n+r(\pi -a)}\sqrt{1+\left (\frac{msin(\frac{(\pi -a)t}{n+r(\pi -a)}+a)(\pi -a)}{n+r(\pi -a)} \right )^2}dt$

Saya tidak akan menghitung integral ini secara manual, disini komputer akan sangat membantu. Adalah lebih baik jika saya langsung menerapkan hasil ini pada contoh spesifik, dan meskipun demikian kita akan mendapati bahwa integral ini masih sulit dihitung, sehingga saya hanya akan menyajikan nilai pendekatannya saja.

Contoh Spesifik

Masalah khusus

Jika roda yang dimaksud dikondisikan seperti ini, maka kita dapati bahwa,

$n=r=4cm$

$m=4\sqrt{2}cm$

$a= \frac{\pi}{4}rad$

$a(t)=(\frac{\pi -\frac{\pi}{4}}{n+r(\pi -\frac{\pi}{4})}) t+\frac{\pi}{4}= (\frac{\frac{3\pi}{4}}{4+4(\frac{3\pi}{4})}) t+\frac{\pi}{4}$

$x(t)=t$

$y(t)=4-4\sqrt{2}cos(a(t))=4-4\sqrt{2}cos((\frac{\pi -\frac{\pi }{4}}{4+4(\pi -\frac{\pi }{4})}) t+\frac{\pi }{4})$

$x'(t)=1$

$y'(t)=\frac{4\sqrt{2}sin(\frac{(\pi -\frac{\pi }{4})t}{4+4(\pi -\frac{\pi }{4})}+\frac{\pi }{4})(\pi -\frac{\pi}{4})}{4+4(\pi -\frac{\pi}{4})}$

$0\leq t\leq 4+4(\pi -\frac{\pi }{4})\equiv 0\leq t\leq 4+3\pi$

Sebelum perhitungan lanjutan dilakukan, ada baiknya saya mengecek apakah kurva kita ini telah dengan benar merepresentasikan keadaan sebenarnya. Untuk itu saya perlu sesuatu yang lebih dari kalkulator grafik. Setelah input dengan benar diketik, berikut outputnya.

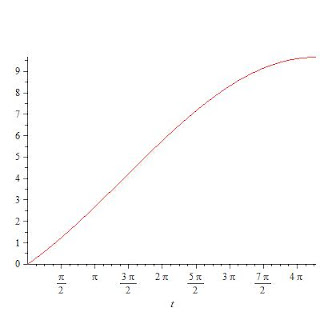Separuh bagian sikloid diplot dengan Maple 15

Jadi,

$L=\int_{0}^{4+3\pi}\sqrt{1+\left ( \frac{4\sqrt{2}sin(\frac{(\pi -\frac{\pi }{4})t}{4+4(\pi -\frac{\pi }{4})}+\frac{\pi }{4})(\pi -\frac{\pi}{4})}{4+4(\pi -\frac{\pi}{4})} \right )^{2}}dt$

Jelas ini bukan suatu integral yang dapat dengan mudah dihitung secara manual, sehingga dengan bantuan komputer (dalam hal ini Wolfram Alpha), didapat:

(Sumber: http://www.wolframalpha.com/)

Maka disimpulkan bahwa, untuk roda dengan jari-jari 4cm dengan batang sepanjang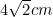 $\inline 4\sqrt{2}cm$ panjang jejak yang akan dibentuk kira-kira 33,7361 cm.
Hasil ini meskipun tidak eksak namun sudah cukup memuaskan, karena 33,7361 cm tidak melebihi 42.176 cm yang merupakan panjang busur separuh lingkaran dengan jari-jari $\inline (4+3\pi )\pi$ .

Correct me if i am wrong!

Barisan (sequence) didefinisikan sebagai suatu susunan objek, khususnya bilangan, baik itu terbatas atau terhitung, sehingga memungkinkan korespondensi satu-satu dengan subset bilangan asli. Barisan yang paling sederhana adalah barisan aritmatika. Barisan ini didefinisikan sebagai suatu susunan bilangan dengan pola tertentu yang mana selisih antara dua suku yang berurutan selalu konstan.

Pola gerakan seorang pemain golf dapat dipandang sebagai barisan (sequence)

Implikasi dari definisi memungkinkan kita menentukan satu anggota barisan aritmatika pada posisi yang spesifik dengan suatu persamaan matematika, yang saya yakin sebagian dari kita sudah familiar dengan persamaan yang dimaksud. Namun bila tidak, ia umumnya dinyatakan sebagai berikut:

Misalnya a sebagai bilangan pertama dalam barisan aritmatika dan b adalah selisih antara dua suku yang berurutan, maka Un adalah suku ke-n dari barisan, yang dinyatakan sebagai:

$U_{n}=a+(n-1)b$

Contohnya, barisan bilangan genap berikut,

$12, 14, 16, 18,. . .$

diketahui bahwa a=12 dan b=2, jadi suku ke-6 dihitung dengan,

$U_{n}=12+(n-1)2=12+2n-2=2n+10$

$U_{6}=2(6)+10=22$

Sebagian dari anda mungkin tidak asing dengan bilangan dalam pola ini

Namun bagaimana dengan barisan aritmatika yang sepertinya bukan barisan aritmatika (polanya belum terlihat dengan sekali saja menghitung selisih dari dua suku berurutan) perhatikan contoh dibawah ini,

$4, 7, 12, 19, 28,...$

Barisan seperti ini susunan bilangannya tidak secara langsung sesuai dengan definisi, namun apabila dianalisis lebih lanjut ternyata, selisih dari tiap dua suku berurutannya justru membentuk barisan aritmatika, perhatikan bahwa perlu dua kali perhitungan untuk melihat baris ini mengikuti definisi :

$\begin{matrix} I & &&& 2 & 2& 2\\ II &&& 3&5 & 7& 9\\ III &&4& 7 & 12 & 19& 28 \end{matrix}$

(Perhatikan : tiap bilangan pada baris baru merupakan selisih dua suku berurutan baris dibawahnya)
Untuk menentukan Un dari barisan seperti ini (kita sebut saja "barisan bertingkat") dapat digunakan persamaan berikut:

$<a_{n}>=a_{n}+(n-1)a_{n-1}+\frac{(n-1)(n-2)}{2!}a_{n-2}+\frac{(n-1)(n-2)(n-3)}{3!}a_{n-3}+...+\frac{(n-1)(n-2)...(1)}{(n-1)!}a_{1}$

yang mana n disini menyatakan banyak tingkat dari barisan awal hingga didapat pola aritmatik dan $\inline a_{n}$ merupakan suku awal tiap tingkat.
Jadi untuk barisan bilangan diatas akan didapat persamaan sebagai berikut:

$<4>_{n}=4+(n-1)3+\frac{(n-1)(n-2)}{2!}2$

yang mana setelah disederhanakan akan diperoleh:

$<4>_{n}=U_{n}=n^{2}+3$

Bukti bahwa persamaan umum diatas tidak jatuh begitu saja dari langit dapat anda pelajari dalam bukti dibawah ini:

Misalkan suatu barisan bertingkat dengan suku awal tiap tingkat masing-masing $\inline a_{1}, a_{2}, a_{3},..., a_{n}$ yang mana barisan pada tingkat pertama merupakan barisan konstan dengan suku $\inline a_{1}$ , maka dapat dibuat suatu daftar susunan barisan-barisan bilangan sebagai berikut,

$\inline \begin{matrix} a_{1}& a_{1} & a_{1} & a_{1}&a_{1}&a_{1} \\ a_{2}& a_{2}+a_{1} & a_{2}+2a_{1} & a_{2}+3a_{1} & a_{2}+4a_{1}&a_{2}+5a_{1}\\ a_{3}& a_{3}+a_{2} & a_{3}+2a_{2}+a_{1} & a_{3}+3a_{2}+3a_{1} & a_{3}+4a_{2}+6a_{1}&a_{3}+5a_{2}+10a_{1}\\ a_{4}& a_{4}+a_{3} & a_{4}+2a_{3}+a_{2} & a_{4}+3a_{3}+3a_{2}+a_{1} & a_{4}+4a_{3}+6a_{2}+4a_{1}&a_{4}+5a_{3}+10a_{2}+10a_{1}\\ .& . & .& . &. &.\\ .& .& . &. &. &.\\ a_{n}& a_{n}+a_{n-1} & . & . &.&. \end{matrix}$

Jika kita cermati, barisan yang dibangun oleh $\inline a_{1}$ adalah baris paling atas dan juga trivial dari daftar kita, sehinga persamaan untuk $\inline a_{1}$ adalah:

$<a_{1}>=a_{1}$

barisan yang dibangun oleh $\inline a_{2}$ tidak lain merupakan barisan aritmatika pada definisi kita, perhatikan koefisien dalam tiap sukunya.

$\inline <a_{2}>=a_{2}+(n-1)a_{1}$

pada barisan yang dibangun oleh $\inline a_{3}$ tugas kita hanyalah menemukan persamaan yang tepat untuk menyatakan tiap koefisien, jika kita cermati $\inline a_{2}$ baru muncul pada suku ke-2 dan $\inline a_{1}$ pada suku ke-3, jadi pola ini dapat dinyatakan sebagai berikut.

$<a_{3}>=a_{3}+(n-1)a_{2}+\frac{(n-1)(n-2)}{2!}a_{1}$

yang apabila proses ini dilanjutkan hingga $\inline a_{n}$ kita akan berakhir pada persamaan umum yang dinyatakan sebelumnya.

Mathematics notes

Translate

Minggu, 02 Desember 2012

Sikloid Variation Problem

Senin, 12 November 2012

Generalisasi Barisan Aritmatika