There are infinitely many primes

mungkin dibutuhkan super komputer untuk membuktikan 

bahwa bilangan yang ditulis gadis ini adalah

bilangan prima tersebut

Teorema fundamental dalam Aritmatika berdiri diatas konsep besar yang kita kenal dengan bilangan prima, dan nyatanya hampir setiap aspek dalam Teori Bilangan merupakan penerapan konsep bilangan prima. Bilangan prima telah dikenal sejak 6500 SM, seperti yang kita ketahui merupakan suatu bilangan asli mulai dari 2, yang hanya habis terbagi oleh 1 dan bilangan itu sendiri. Secara formal definisi bilangan prima dapat dinyatakan sebagai berikut:

"Suatu bilangan bulat 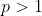 dikatakan prima jika pembagi positifnya hanya 1 dan . Suatu bilangan lebih dari 1 yang bukan prima dinamai komposit".

Diantara sepuluh bilangan bulat pertama, 2, 3, 5, dan 7 adalah prima sedangkan 4, 6, 8, 9 dan 10 komposit.

Tidak seperti beberapa jenis bilangan yang polanya dapat diformulasi sebagai contoh bilangan genap berpola 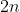, ganjil 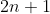dan kuadrat  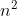dimana 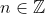, bilangan prima tidak memiliki pola unik yang dapat dituliskan dalam sebaris persamaan matematika. 2200 tahun lalu Eratosthenes dari Cyrene  (276-194 SM)  memberikan suatu algoritma yang sederhana untuk mencari bilangan prima yang lebih kecil dari suatu bilangan yang diberikan, sayangnya algoritma yang dinamai Saringan Eratosthenes ( Sieve of Erastosthenes ) ini tidak efektif jika bilangan yang diberikan cukup besar.

bilangan dalam sel-sel putih merupakan

bilangan prima

Telah banyak matematikawan terdahulu mencoba memformulasikannya, namun terbukti gagal. Salah satu yang cukup fenomenal adalah Mersenne Prime, yaitu bilangan yang mengambil bentuk:

Yang oleh pembuatnya Father Marine Marsenne dibuku yang berjudul Cogitata Physica-Mathematica (1644) menyatakan bahwa 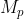 adalah prima untuk  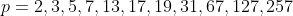dan komposit untuk semua bilangan prima  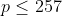lainnya. Mersenne Prime bertahan 300 tahun hingga 1903 Frederick Nelson Cole melakukan perhitungan manual panjang dan senyap di American Mathematical Society meeting untuk menunjukan bahwa 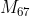 komposit. Kabar yang beredar mengatakan butuh 20 tahun bagi Frederick secara rutin ditiap minggu sore mencari faktor dari  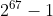yang jika dijabarkan terdiri dari 21 digit. Selain itu adapula Fermat Number, yaitu bilangan dalam bentuk:



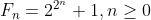
yang kemudian ditunjukan oleh  Leonhard Euler bahwa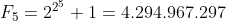  terbagi oleh 641.

Ketidak-teraturan ini yang membuat bilangan prima mendapat tempat khusus dalam matematika, khususnya pada Teori Bilangan.  Telah banyak nama-nama matematikawan besar yang berkerja dengan bilangan prima, sebut saja Leonhard Euclid, Bernhard Riemann dan Carl Friedrich Gauss, semua dengan hasil temuan yang banyak berpengaruh pada apa yang sekarang kita kenal dengan Teori Bilangan.

Seperti kita ketahui  berorde tak-hingga, sehingga karena bilangan prima anggota himpunan  maka cukup masuk diakal bila ia juga berorde tak-hingga, sayang sekali penalaran seperti ini pastilah ditolak mentah-mentah bila dinyatakan dalam ruang lingkup akademis. Untuk membuktikan bahwa ada tak-hingga banyaknya bilangan prima, Euclid 2000 tahun lalu telah melakukan pembuktian yang sangat memuaskan untuk itu dengan kontradiksi.

( Euclide 365-300 SM)

Berikut bukti lengkapnya:

Misalkan 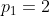, , 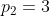,, 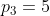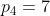. . . merupakan barisan naik bilangan prima, dan misalkan ada bilangan prima terakhir dalam barisan ini, yaitu .

Sekarang pandang bilangan bulat positif;

karena 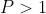 dan komposit, maka  pastilah terbagi oleh salah satu bilangan prima dalam daftar (barisan),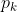. Disini bisa kita pahami bahwa  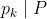dan 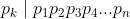. Dengan mengkombinasikan kedua relasi yang barusan kita sampai pada relasi  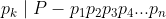dengan kata lain 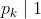. Seperti diketahui bahwa pembagi bulat dari 1 adalah 1 itu sendiri dan 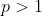memunculkan kontradiksi.

Jadi tidak ada daftar lengkap dari bilangan prima, dengan kata lain ada tak-hingga banyaknya bilangan prima.          Q.E.D

Bukti asli dari Euclide dapat dibaca dalam book IX dari Element Proposisi 20.

Meskipun telah dibuktikan bahwa tidak mungkin menemukan rumus eksplisit untuk pola bilangan prima, matematikawan tidak berhenti sampai disitu, kini perhatian dialihkan pada distribusi bilangan prima, yang mana diharapkan merupakan kunci penting untuk membuktikan Riemann Hypothesis ( masalah ke-6 dari 7 masalah milenium ).